日常の生活の中で、「A」や「B」、または「選択をしない」。
などの状況は多々あります。
その時に確率的になにが正しいのかを知る必要があります。
それを知った上で、
どのような選択をするかは自由だと思います。
どちらが確立的に正しいかを知らず、決めるのは
かなりもったいないです!
その情報が事前に入っていれば、選択が変わっていた( ;∀;)
などと後でいってもはじまりません。
なので今回の記事は
ある事象において、
確率的にどちらが正しいのかを知る
を目的として問題をいくつか用意してみました。
頭の体操と思って、時間がある時に少しずつ読み進めてみて下さい。
問題:サンプル数の重要差
学校の生徒会選挙には2人の候補、AさんとBさんが出ています。
選挙の前日にランダムに100人の生徒にアンケートを取ったところ、以下の結果が得られました。
- Aさんを支持する生徒:55人
- Bさんを支持する生徒:45人
このアンケート結果を基に、明日の選挙でAさんが勝つ確率がBさんが勝つ確率よりも高いと言えるか、それとも決定的ではないか、以下の選択肢から正しいものを選んでください。
- Aさんが勝つ確率が高い。
- Bさんが勝つ確率が高い。
- アンケート結果からは、どちらが勝つか決定的には言えない。
答え:
- アンケート結果からは、どちらが勝つか決定的には言えない。
解説:
アンケートの結果、Aさんの支持率が高いように見えますが、サンプルサイズ(100人)と全体の生徒数によって結果が変わる可能性があります。
また、選挙当日に心変わりする生徒や、アンケート時に本音を言わなかった生徒も考えられるため、このアンケート結果だけからは勝者を確定的に予想することはできません。
このようなトリックはよくあります。
アンケート100人とって、Aさんが多いからAさんだよ。
と答える人!
いちいち、反論する必要はありませんが、
「確率が分かっていない人だからこの人の話は参考にならない」
と思い、自己防衛をして下さい。
問題: 「誕生日の逆の問題」
あるクラスには、生徒が30人います。
教師は、このクラスの中で誕生日が同じ日の生徒が1組以上いる確率について質問をしました。
A: 30人の中で、誕生日が同じ日の生徒が1組以上いる確率は50%以上である。
B: 30人の中で、誕生日が同じ日の生徒が1組以上いる確率は50%未満である。
あなたはAとBの中から、確率的に正しい選択肢を選ぶべきです。
どちらが正しいでしょうか?
答え:
A: 30人の中で、誕生日が同じ日の生徒が1組以上いる確率は50%以上である。
が答えとなります。
これは統計学の授業を受けた方であれば一度は聞いたことがある例だと思います。
実際のところ、この問題は「誕生日の逆の問題」として知られており、直感に反して30人の中で誕生日が同じ日の生徒が1組以上いる確率は70%以上となります。
したがって、答えはAです。
しかし、多くの人々は直感的に30人の中で2人以上の誕生日が同じ日になる確率は低いと感じるため、Bを選んでしまうことが多いです。
詳しい解説
興味ある方は引き続きこの問題の背後にある確率的考察をお読みください。
「誕生日の問題」は、人々の直感とは逆に、比較的少ない人数でも同じ誕生日を持つ2人がいる確率が高いという事実に基づいています。
この問題を解くためには、まず逆の確率、すなわち「全員の誕生日が異なる確率」を考えるとよいです。
1人目の誕生日は365日のいずれでも構いませんので、確率は 365分の365 と 365分の365では1になります。
2人目の生徒が1人目と異なる誕生日である確率は 365分の364です。
3人目の生徒が前の2人と異なる誕生日である確率は 365分の363 です。
これを30人目まで続けます。
したがって、全員の誕生日が異なる確率は以下のように計算されます:
P(異なる誕生日)=365分の365分×365分の364分×365分の363・・・・・・・・と続きます。
全員の誕生日が異なる確率を求めた後、少なくとも2人が同じ誕生日を持つ確率は、以下のように計算できます。
P(同じ誕生日)=1−P(異なる誕生日)
この計算を行うと、30人の中に少なくとも1組以上の生徒が同じ誕生日である確率が70%以上であることがわかります。
この方法で確率を計算すると、直感とは異なる結果が得られることが多いため、「誕生日の問題」として知られるようになりました。
実際に自分でエクセルで計算してみると思いますです。
問題:みんなコーヒー大好き
ある町に2つのカフェがあります。
カフェAでは、お客さんに無料でコーヒーを提供しており、
カフェBでは、お客さんに無料で紅茶を提供しています。
ある日、この町に100人の訪問者がやってきました。全員がカフェを訪れることになります。
以下の情報を基に、訪問者がコーヒーを好む確率が高いと思われるのは、AかBかで答えなさい。
- この町の住民の70%がコーヒーを好み、30%が紅茶を好みます。
- 訪問者の中で、カフェAを最初に訪れる人は40人、カフェBを最初に訪れる人は60人です。
答え:
答えはカフェBの紅茶屋さんです。
恐らく多くの人は、町の住民の好みを基に答えを「カフェA」とするかもしれません。
しかし、この問題では訪問者の好みは直接与えられていない点に注意が必要です。
実際のところ、どちらのカフェを訪れるかの選択は、訪問者の飲み物の好みとは無関係に決定されるかもしれません。
従って、訪問者がコーヒーを好む確率については、提供された情報から正確に判断することはできません。
ただ、問題文中の情報からは、カフェBを訪れる訪問者の数が多いため、
選ぶ基準としてはBが適していると言えるでしょう。
この問題は、情報の解釈や認識の偏りを誘導することで、多くの人がAと答えるような問題になっています。
余計な情報を相手に与えることで、勘違いする傾向があります。
問題:こんなのよくある
太郎くんは、2つの袋を持っています。
袋Aには、赤い玉が3個、青い玉が2個入っています。
袋Bには、赤い玉が5個、青い玉が3個入っています。
太郎くんが袋Aから1個の玉を無作為に取り出す場合と、袋Bから1個の玉を無作為に取り出す場合、どちらの袋の方が赤い玉を取り出す確率が高いでしょうか?
A. 袋A
B. 袋B
C.どちらも同じ
答え:
袋Bとなります。
直感的にAが多い、もしくはどちらも同じ!っと答えるかたが多いです。
しかし計算してみてると、
袋Aから赤い玉を取り出す確率: P(袋Aの赤い玉)=3+2分の3は5分の3なので、0.6になります。
一方、袋Bから赤い玉を取り出す確率: P(袋Bの赤い玉)=3+5分の5は8分の5なので
0.625。
以上のことから、袋Bから赤い玉を取り出す確率の方がわずかに高いです。
一見、袋Aの方が赤い玉の割合が多いように見えますが、計算すると袋Bの方が確率的に赤い玉を取り出す確率が高いことがわかります。
この問題は直感とのギャップがあるため、答えるのが難しいと感じるかもしれません。
実際日常生活でも、0.6と0.625程度であれば、よくわからないまま判断することはあると思いますが、
そんなに難しい計算ではないです。
常に確率はどのような計算したら最適解を見つけることが出来るかのポイントを知ることが大事です。
問題: あえてする必要がある
田中さんは株式投資を始めることを決意しました。彼は友人から以下の二つのアドバイスを受けました。
A) 過去1年間で最も成果を上げた株を買うとよい。
B) まずは幅広く分散投資をして、リスクを分散させるべきだ。
田中さんが長期間で安定してリターンを得るために選ぶべきアドバイスはどちらでしょうか?
2択で回答お願いします。
答え:
B) まずは幅広く分散投資をして、リスクを分散させるべきだ。
となります。
【解説】
過去のパフォーマンスは未来の結果を保証するものではありません。
一年前に最も成果を上げた株が、これからも同じように成果を上げ続けるとは限らないため、Aの方法はリスクが高くなります。
一方、分散投資は多くの株に投資することで、一つの株が大きく下がっても他の株がその損失を相殺する可能性があり、リスクを軽減できます。
よってBのアドバイスが長期的にはより安全と考えられます。
この問題は、過去の成功に引きずられやすい人々の心理を利用しています。
多くの人は短期間の成功を重視し、それを未来の成功の指標として認識してしまいがちです。
しかし、投資の世界では長期的な視点が重要であり、短期間の成功よりもリスクの分散が大切です。
あともう1点大事なポイントは2択というところです。
あくまでも、AとBではBの方が安全というだけで、CやDなどの選択肢がある場合は内容次第ではそちらが良いかもしれません。
AとBという選択肢の中ではBがより安全ではありますが、それ以外の選択肢も常にあるということを頭に入れておく必要があります。
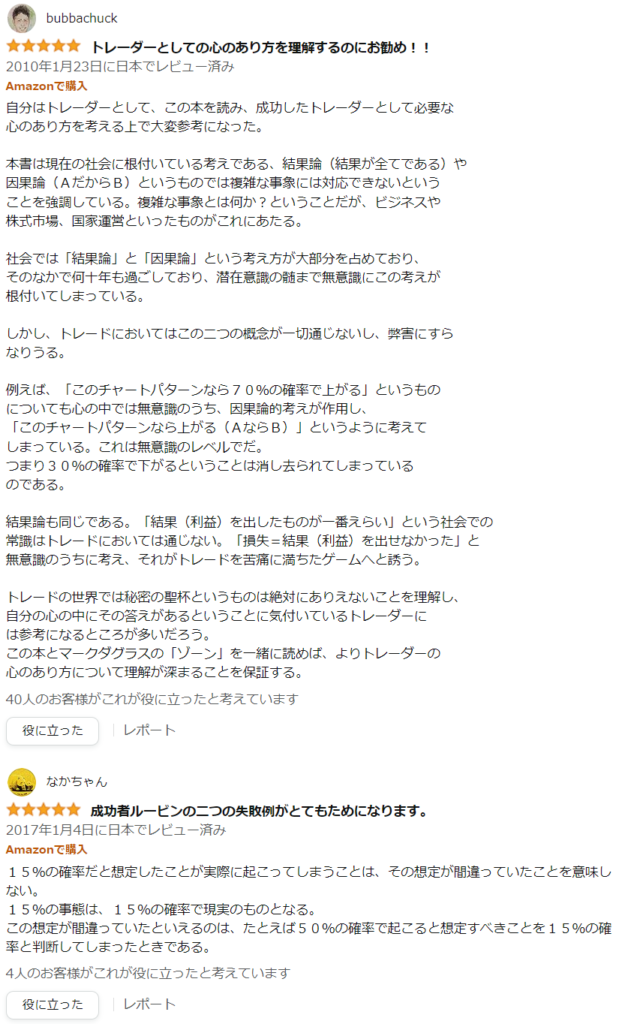
著者である、田渕 直也さんもバリバリの金融畑の方で投資に関するものは様々出されており、10回は読まないと理解しにくい書籍から、さらっと読めるものまであります。
その中でこの確率論的思考はサクッと読めるだけでなく、楽しく読み進められます。
レビュー元:アマゾンよりhttps://amzn.to/47JFr25